Special Project: Generalized Pythagoras Trees

In my special project (2013) at University of Stuttgart I was working on Hierarchy Visualization with Generalized Pythagoras Trees. This is a topic from the area of information visualization.

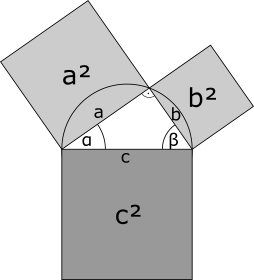
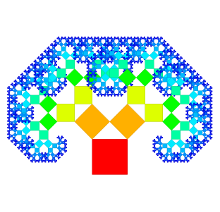
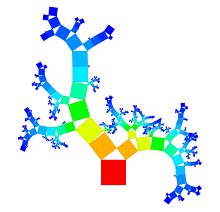
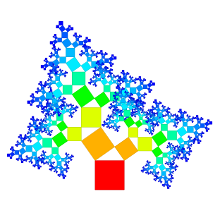
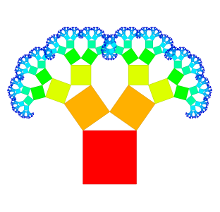
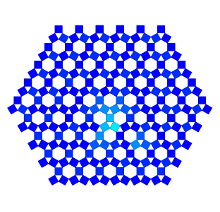
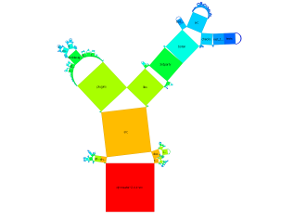
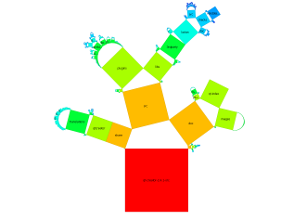
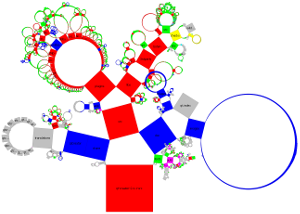
Goal of this work was the development of a new visualization technique for arbitrary hierarchical structures by expanding Pythagoras Trees. These trees are fractals, consisting of squares that are connected by right-angled triangles. They can be used to represent hierarchies by assuming that each square represents a node. These traditional Pythagoras Trees have a branching factor of two. They were extended to represent hierarchies with any branching factor. This new approach uses rectangles to visualize nodes. As connections between nodes, convex polygons are used, thus not necessarily right-angled triangles as commonly used by traditional Pythagoras Trees. Different variations for the visualizations of hierarchies can be created by changing the width, height, arrangement and color of rectangles. The corresponding interactive application for the visualization technique is implemented in C++; Qt is used for the user interface and the Qt Graphics View Framework for graphical and interactive elements of the visualization. The Doxygen format is used for documentation. It is possible to process directory structures as well as files in the Newick format to create visualizations.

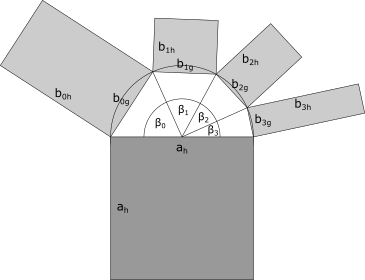
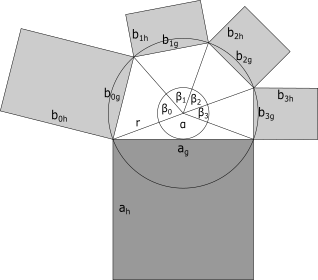
The following images show the principles for constructing both types - traditional and generalized Pythagoras Trees. For the generalized trees two versions can be differentiated: sub nodes can be connected to their parent node with either a semicircle or a circle.

I started my project with a detailed study of traditional Pythagoras Trees. Below, there are some results I received by changing properties of the triangles. For the first few images right-angled triangles are used, for the latter ones isosceles triangles (with different angles respectively).

This video shows different tree representations for traditional Pythagoras Trees created by changing parameters in the corresponding application:

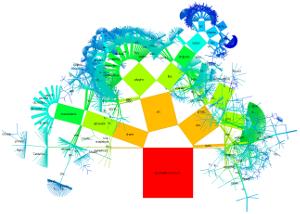
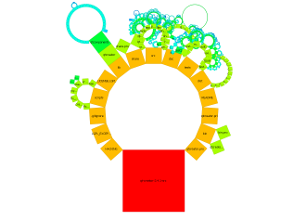
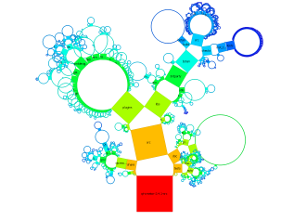
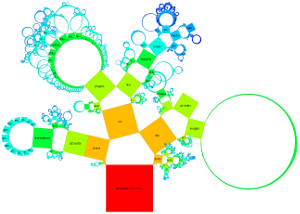
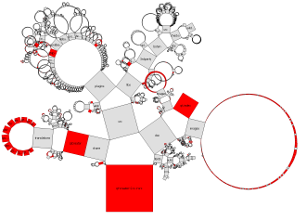
Below, for generating generalized Pythagoras Trees the directory structure of the source code of the Qt Creator is used as hierarchy.

The arrangement of nodes in a generalized Pythagoras Tree is either on a semicircle or a circle. The size of nodes is either the same for each node with the same depth, related to the number of leaf nodes or to file/directory sizes. The nodes can be represented as squares or more generalized as rectangles. Depending on the settings chosen it is possible to get the sum of the surface areas to be the same for each depth.

Examples for the search function and coloring by categories of file extensions (of leaf nodes):

In this video different ways to visualize the data are presented as well as interactive features such as the search function, the highlighting of categories and semantic and geometric zooming:

The results of this project were published in two publications: In Generalized Pythagoras Trees for Visualizing Hierarchies and Generalized Pythagoras Trees: A Fractal Approach to Hierarchy Visualization.