Studienarbeit: Verallgemeinerte Pythagorasbäume

In meiner Studienarbeit (2013) an der Universität Stuttgart habe ich mich mit Hierarchievisualisierung mit verallgemeinerten Pythagorasbäumen auseinandergesetzt. Es handelt sich hierbei um ein Thema aus dem Bereich der Informationsvisualisierung.

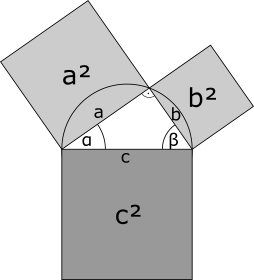
Ziel dieser Arbeit war die Entwicklung einer neuen Visualisierungstechnik für beliebige hierarchische Strukturen durch die Erweiterung von Pythagorasbäumen. Pythagorasbäume sind Fraktale, die aus Quadraten bestehen, welche über rechtwinklige Dreiecke miteinander verbunden sind. Sie können zur Darstellung binärer Hierarchien verwendet werden, indem jedes Quadrat als Knoten aufgefasst wird. Diese traditionellen Pythagorasbäume besitzen einen Verzweigungsgrad von zwei. Sie wurden so erweitert, dass sie auch Hierarchien mit beliebigem Verzweigungsgrad darstellen können. Dieser neue Ansatz verwendet für die Knotendarstellung Rechtecke. Als Verbindungselemente zwischen den einzelnen Knoten kommen konvexe Polygone, also nicht zwingend rechtwinklige Dreiecke wie beim traditionellen Pythagorasbaum üblich, zum Einsatz. Verschiedene Varianten der Abbildung für die Hierarchien können erzeugt werden durch Veränderung von Breite, Höhe, Anordnung und Farbe der Rechtecke. Die zugehörige interaktive Anwendung zur Visualisierungstechnik ist in C++ implementiert; Qt wird für die Benutzeroberfläche verwendet und das Qt Graphics View Framework für die grafischen und interaktiven Elemente der Visualisierung eingesetzt. Das Doxygen-Format wird zur Dokumentation genutzt. Es können sowohl Verzeichnisstrukturen, als auch Dateien, die im Newick-Format vorliegen, als Grundlage für die Visualisierungen verwendet werden.

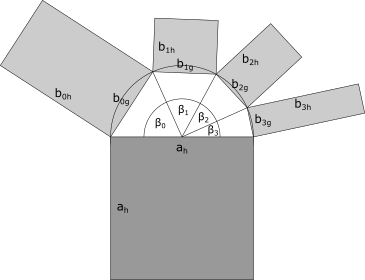
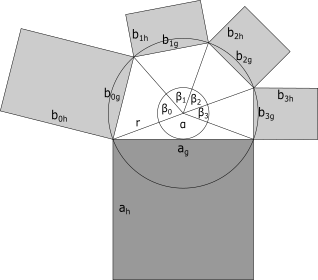
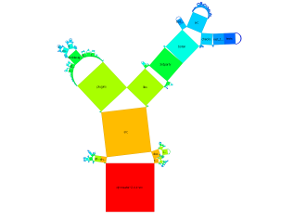
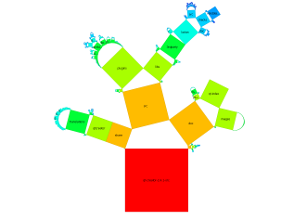
Die folgenden Abbildungen zeigen die prinzipiellen Konstruktionsweisen für beide Arten - die traditionellen und die verallgemeinerten Pythagorasbäume. Bei den verallgemeinerten Bäumen können zwei Varianten unterschieden werden, wobei Unterknoten mit ihren Elternknoten entweder um einen Halbkreis oder einen vollständigen Kreis angeordnet sind.

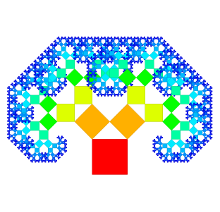
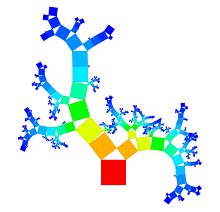
Das Projekt wurde mit einer ausgiebigen Untersuchung traditioneller Pythagorasbäume begonnen. Nachfolgend sind einige Ergebnisse zu sehen, die ich durch Veränderung der verbindenden Dreiecke erhalten konnte. Bei den ersten Bildern werden rechtwinklige Dreiecke verwendet während bei den folgenden gleichschenklige Dreiecke eingesetzt werden (mit jeweils unterschiedlichen Winkeln).

Dieses Video zeigt die zugehörige Anwendung mit traditionellen Pythagorasbäumen, wo durch Veränderung verschiedener Parameter unterschiedliche Baumdarstellungen erzeugt werden können:

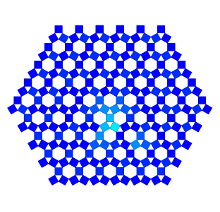
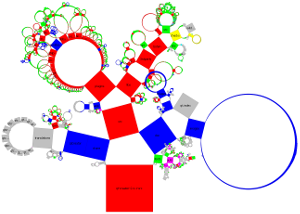
Für verallgemeinerte Pythagorasbäume wird nachfolgend die Verzeichnisstruktur für den Quellcode des Qt Creators als Hierarchie verwendet.

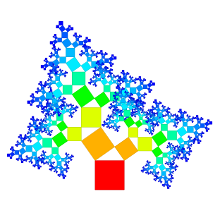
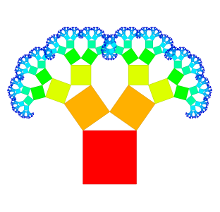
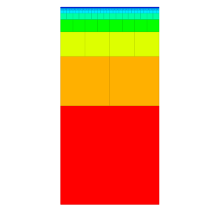
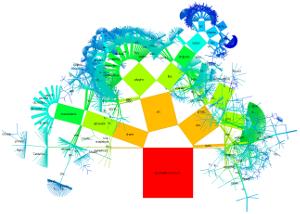
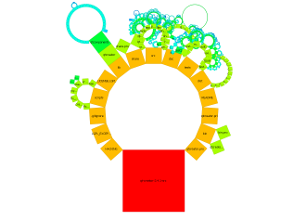
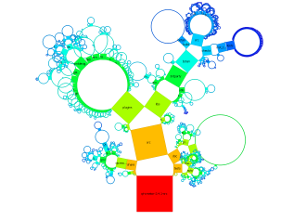
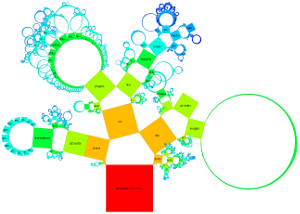
Bei verallgemeinerten Pythagorasbäumen erfolgt die Anordnung der Knoten entweder um einen Halbkreis oder Kreis. Die Größe der Knoten ist entweder gleich für alle Knoten einer Tiefe, in Abhängigkeit der Anzahl an Blattknoten oder in Abhängigkeit von Datei-/Verzeichnisgrößen. Die einzelnen Knoten können als Quadrate dargestellt werden oder verallgemeinert als Rechtecke. Je nach Wahl der Kriterien kann erreicht werden, dass die Summe der Flächeninhale aller Rechtecke einer Tiefe jeweils dieselbe ist. Dies sind einige mögliche Darstellungsarten:

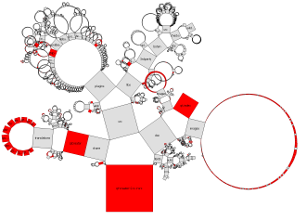
Beispiele für die Suchfunktion und eine Einfärbung nach Kategorien, welche aus Dateiendungen (von Blattknoten) gebildet werden:

Im Video werden verschiedene Arten für die Darstellung der Daten präsentiert sowie interaktive Funktionen wie die Suchfunktion, das Anzeigen von Kategorien und semantisches und geometrisches Zoomen demonstriert:

Die Ergebnisse dieses Projekts wurden in zwei Publikationen veröffentlicht: In Generalized Pythagoras Trees for Visualizing Hierarchies und Generalized Pythagoras Trees: A Fractal Approach to Hierarchy Visualization.